[2021년 08월 15일 21시 08분 작성]
[PS][백트래킹]
BOJ 1079 : 마피아
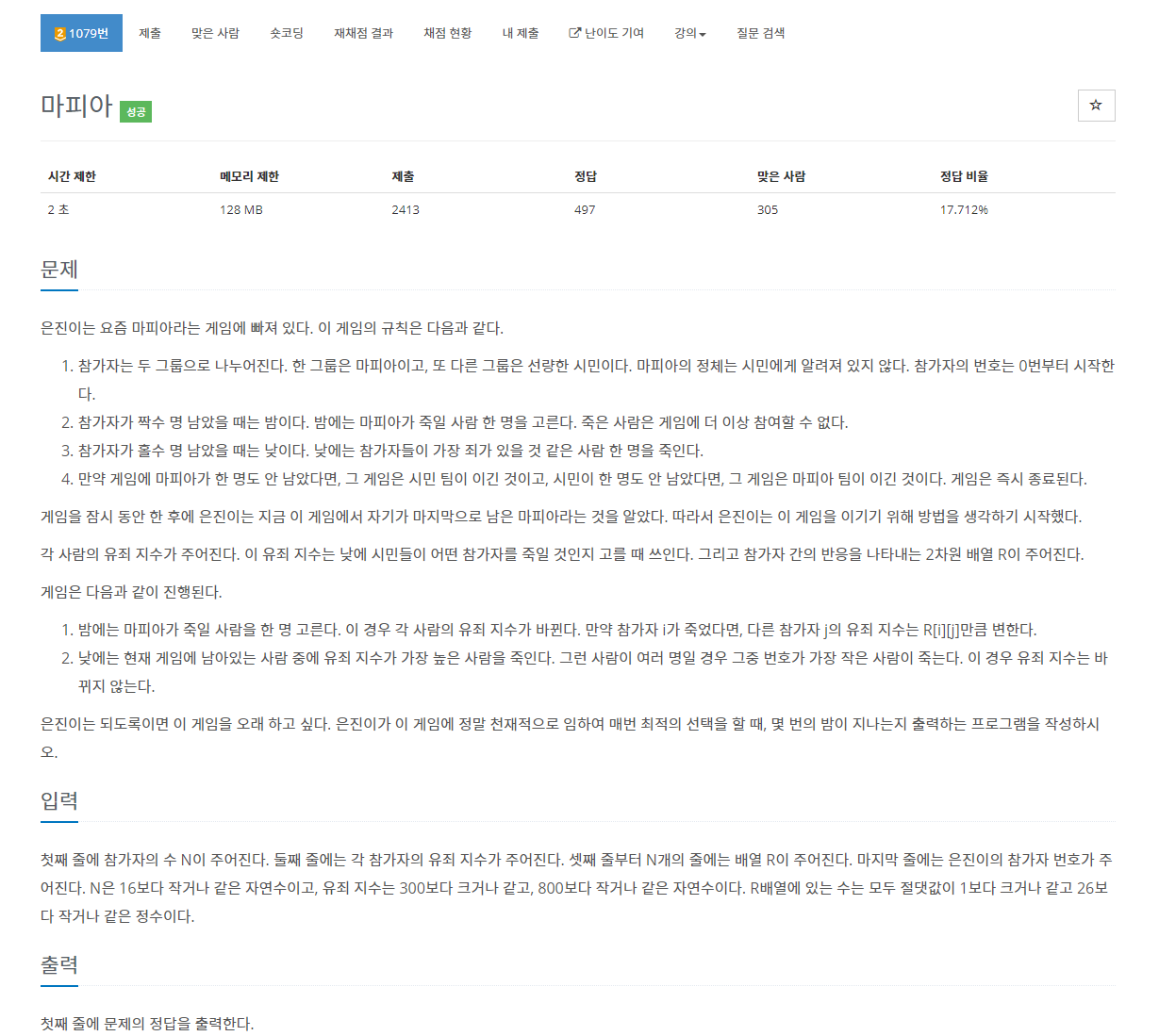
[문제 링크 : 클릭]
1. 풀이
백트래킹을 이용한 문제입니다.
함수 정의를 다음과 같이 두고,
| Solve(cnt) = 남은 사람이 cnt명, 최대로 보내는 밤의 횟수 |
각 조건에 맞게 코드를 작성해주면 해결할 수 있습니다.
자세한 설명은 코드에 주석으로 남겨두었습니다.
+) 유의할 점
가장 오래 마피아가 버티는 경우는 마피아가 이기는 경우입니다.
즉, 위 함수에서 남은 사람이 1인 경우가 바로 정답입니다.
이 문제는 시간 제한이 있기 때문에, cnt가 1인 경우를 찾는 즉시 남은 경우들을 넘겨야 합니다.
2. 소스코드
[Github 링크 : 클릭]
#include <bits/stdc++.h>
using namespace std;
int n, mafia, state = (1<<17);
bool flag = false;
vector<int> g;
vector<vector<int> > r;
int Solve(int idx, int state, int cnt);
inline bool isDead(int idx)
{
if(state & (1<<idx)) return true;
return false;
}
int Solve(int cnt)
{
if(flag) return 0;
if(isDead(mafia) || cnt==1) //마피아 혼자 살아남거나, 마피아가 죽은 경우라면 반환
{
flag = (cnt==1); //만약, 마피아 혼자 남는다면? 다른 모든 경우는 고려하지 않음
return 0;
}
int ret = 0;
if(cnt%2) //짝수 : 낮의 경우
{
int g_val=-1, g_idx=-1;
for(int i=0; i<n; i++) //최대 유죄 지수인 사람을 찾음
{
if(isDead(i)) continue; //이미 죽은 사람은 고려x
if(g_val < g[i])
{
g_idx = i;
g_val = g[i];
}
}
state |= (1<<g_idx); //그 사람을 죽임
ret = max(ret, Solve(cnt-1)); //다음 경우를 고려
state &= ~(1<<g_idx); //백트래킹
}
else //홀수 : 밤의 경우
{
for(int i=0; i<n; i++)
{
if(i==mafia || isDead(i)) continue; //마피아 본인과, 이미 죽은사람 고려x
state |= (1<<i); //i번째 사람을 죽임
for(int j=0; j<n; j++) g[j] += r[i][j]; //+) 유죄 지수 갱신
ret = max(ret, Solve(cnt-1)+1); //다음 경우를 고려
for(int j=0; j<n; j++) g[j] -= r[i][j];
state &= ~(1<<i); //백트래킹
}
}
return ret;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
cin>>n;
g = vector<int>(n, 0);
r = vector<vector<int> >(n, vector<int>(n, 0));
for(int i=0; i<n; i++)
cin>>g[i];
for(int i=0; i<n; i++)
for(int j=0; j<n; j++)
cin>>r[i][j];
cin>>mafia;
cout<<Solve(n)<<'\n';
return 0;
}3. 반성
- 최대를 구해준다면서.. 변수를 999로 초기화를 해놨었네요.
- 괜히 다른 멀쩡한 부분만 자꾸 건들면서 오답 파티를 벌였습니다.

- 제출은 신중하게, 코드 분석도 차근차근..
'PS > BOJ' 카테고리의 다른 글
| [PS][구현] BOJ 17480 : 개구쟁이 준석이 (0) | 2021.08.14 |
|---|---|
| [PS][DP] BOJ 17485 : 진우의 달 여행(Large) (0) | 2021.08.13 |
| [PS][완전탐색] BOJ 17484 - 진우의 달 여행(Small) (0) | 2021.08.13 |
| [PS][자료구조] BOJ 17479 : 정식당 (0) | 2021.08.13 |
| [PS][재귀] BOJ 17478 : 재귀함수가 뭔가요? (0) | 2021.08.13 |